دفتر ریاضی

(( در صفحه ی شطرنج و در خانه ی اول ، برای من یک دانه گندم ، در خانه ی دوم دو برابر خانه ی اول و در خانه ی سوم دو برابر خانه ی دوم گندم قرار دهید و به همین ترتیب پیش بروید ))   پادشاه از درخواست او تعجب کرد و دستور داد به او یک کیسه گندم بدهند . به نظر شما ، آیا درخواست مخترع شطرنج به اندازه ی یک کیسه گندم بوده است ؟

جواب :

می توان دانه های روی خانه های صفحه ی شطرنج را به صورت توان های متوالی  ۲  نشان داد :

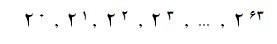
 مجموع این اعداد یک تصاعد هندسی با قدر نسبت  ۲  و جمله ی اول ۱  تشکیل  می دهند :

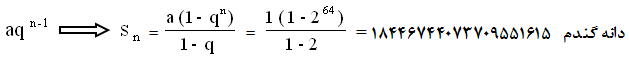
 در یک متر مکعب  تقریبا  ۱۵  میلیون دانه گندم جا می گیرد . بنابراین گندمی که مخترع شطرنج خواسته است تقریبا به ۰۰۰ ۰۰۰ ۰۰۰ ۲۰۰ ۱ متر مکعب یا   ۱۲۰۰ کیلومتر مکعب جا نیاز دارد ،  یعنی انباری که طول وعرض و ارتفاع آن هر کدام برابر با  ۱۲۰۰  کیلومتر باشد . اگر طول انبار را  ۴  متر وعرض آن را  ۲  متر بگیریم ارتفاع انبار باید به اندازه ی  فاصله زمين تا خورشيد باشد !!!

اگر طول انبار را  ۴  متر و عرض آن را  ۱۰  متر بگیریم ، ارتفاع انبار برای ذخیره کردن این مقدار گندم باید  ۸۰  برابر فاصله ی زمین تا ماه باشد !!!

طبق محاسبه دیگری هم برای به دست آوردن این مقدار گندم سطح کره زمین باید ۸ بار زیر کشت گندم برود !!!

ابوریحان بیرونی در کتاب خود به نام آثار الباقیه ، مساله معروف شطرنج را که در واقع مساله ای مربوط به یک تصاعد هندسی است که جمله ی اول آن واحد و تعداد جمله ها ۶۴ می باشد را حل کرده است . و با استدلال دقیق مقدار آن را یه دست آورده است .

ابوریحان بیرونی با استدلال به این نتیجه رسید که مقدار گندم ها برابر ۲ به توان ۶۴ منهای یک می باشد . و برای محسوس کردن این عدد می گوید : در سطح کره زمین  ۲۳۰۵  کوه را در نظر بگیرید، اگر از هر کوه ۱۰۰۰۰ رود جاری شود در طول رودخانه هزار قطار قاطر حرکت کند و هر قطار شامل ۱۰۰۰  قاطر باشد و بر هر قاطر ۸ کیسه گندم قرار داده باشیم ودر هر کیسه ده هزار دانه گندم باشد آن وقت عدد همه ی این گندم ها از تعداد گندم های صفحه ی شطرنج کمتر می شود !!!