دفتر ریاضی

حکایت ریاضیدانان و اعداد اول ، همان حکایت گاوچران ها و اسب های وحشی است . خیلی ها وارد این عرصه شدند اما جزء اندکی ، بقیه کاری از پیش نبردند . یکی از بزرگترین آرزوهای هر ریاضیدانی پیدا کردن فرمولی برای یافتن اعداد اول است . البته هستند کسانی که قانع ترند و به یافتن عدد اول کشف نشده ای راضی اند تا بلکه به نام آنها ثبت شود و یا جایزه ای از آن نصیب شان بشود . اعداد اول بسیار زیبا ، جذاب و در عین حال حیرت انگیز و رام نشدنی هستند .

قضیه خیلی ساده است . اگر از منظر بخشپذیری به اعداد طبیعی بزرگتر از یک نگاه کنیم ، بغضی از اعداد فقط به دو عدد بخشپذیرند ، خودشان و یک . ما به این اعداد ، عدد اول می گوییم . و یا اینطور هم می توانیم آنها را تعریف کنیم : اعدادی که نمی توان آنها را به صورت حصل ضرب دو عدد بزرگتر از یک نوشت . مانند 2 ، 7 ، 41 ، 919 .           بینهایت عدد اول وجود دارد .

حالا ماجرا از همین جا شروع می شود  و سوالات زیر را به وجود می آورد : آیا رفتار آنها در سلسله ی اعداد قابل پیشبینی است ؟ آیا نحوه ی ظاهر شدنشان منظم است ؟ آیا فرمولی کلی برای یافتن آنها وجود دارد ؟ آیا روشی سریع برای تست یک عدد اول وجود دارد ؟ آیا ... .

طی قرن های متمادی ریاضیدانان شرق و غرب ، با انواع روش ها به جستجوی آنها پرداختند ولی پیشرفت کارشان از پیشرفت آزاد راه تهران شمال هم کندتر بوده است . هرچه تعداد بیشتری از آنها شکار می شوند ، کار شکار عدد بعدی دشوارتر می شود . حتی ابر کامپیوترها هم در مقابل این اعداد دست ها را به نشانه ی تسلیم بالا برده اند و اظهار عجز می کنند . حتی اگر میلیون ها بار به سرعت کامپیوترهای فعلی اضافه شود ، باز هم تنها چند رقم به شماره ی بزرگترین عدد اولی که تا کنون شناخته شده است ، افزوده می شود .

اما اهمیت این اعداد در چیست ؟ آیا ریاضیدان ها صرفا از روی کنجکاوی به دنبال آنها می گردند ؟ اگر به کاربرد آنها در ریاضیات بخواهیم بپردازیم ، باید بگوییم که قضیه ی بنیادی حساب در مورد آنهاست و نقش اصلی اعداد اول به عنوان عناصر سازنده ی تمام اعداد صحیح بسیار اهمیت دارد . آنها مانند بلوک های ساختمانی در ساختن سایر اعداد نقش دارند ، یعنی دقیقا همان نقش اتم ها در ساختمان مواد را دارا هستند .

  قضیه ی بنیادی بیان می دارد که : هر عدد طبیعی بزرگتر از یک را می توان به طور یکتا ، به صورت حاصل ضرب اعداد اول نوشت . مانند : 

این قضیه اساسا توسط اقلیدوس به اثبات رسیده است ، اما اولین اثبات کامل از آن توسط گاوس در کتاب تحقیقات حساب منتشر شده است . گاوس اعلام می کند که مساله تشخیص اعداد اول ، یکی از مهمترین مسائل حساب به شمار می آید . 

اما آنها در اقتصاد و تجارت و امنیت هم نقش دارند ! در حال حضر بسیاری از معاملات تجاری و نقل و انتقالات مالی و نیز مبادله ی اطلاعات محرمانه از طریق شبکه های مخابراتی مانند اینترنت ، با بهره گیری از رمز کردن پیام ها به انجام می رسد . اطلاعات حساب های بانکی و کات های اعتباری نیز با استفاده از اعداد اول رمزنگاری می شود . اعداد اول در تنظیم این گونه رمزها نقش اساسی بر عهده دارند . و از این رو دستیابی به عدد اول جدید که دیگران از آن بیخبر باشند برای سازندگان این رمزها و نیز مشتریان آنها از اهمیت زیادی برخوردار است .

 سازندگان كامپیوترها و ارائه‌دهندگان خدمات اینترنتی با توجه به آنكه در حال حاضر افراد بسیاری از فعالیتهای خود را از طریق اینترنت انجام می دهند، نظیر اینكه پول قبضهای برق و آب و تلفن خود را می‌پردازند یا در كلاسهای مورد نظر ثبت نام می‌كنند، یا بلیت هواپیما و قطار رزرو می‌كنند، در تلاشند تا از خطر دستیابی تبهكاران به اطلاعات شخصی افراد جلوگیری به عمل اورند.

علم رمز مدرن بدون شک مدیون خواص بی مانند و جادویی اعداد اول است . معمولی ترین الگوریتمی که برای رمزنگاری نامتقارن استفاده می شود ، الگوریتم  RSA می باشد . این روش پس از کارهای اولیه سه ریاضیدان به نام ریوست ، شامیر و آدلمن در سال 1978 منتشر شد . ایده ی اولیه ی الگوریتم بسیار ساده به نظر می رسد : ضرب اعداد خیلی ساده است ولی تجزیه اعداد بسیار مشکل است .

با این مثال قضیه روشن می شود : اگر دو عدد اول مانند  4575163 = p  و  4093567 = q در نظر بگیریم ، آنگاه به سادگی می توان حاصلضرب آنها یعنی  18728736276421 = pq  را بیابیم . ( حتی با استفاده از روش های مدرسه ای برای ضرب کردن ، که برای یک جفت عدد  n  رقمی در حدود 2n گام زمان می برد ) . حالا اگر عدد 18728736276421 را به کسی بدهیم و از او بخواهیم تا آن را تجزیه کند ، احتمالا در حدود یک میلیون گام ، زمان نیاز دارد . خاصیت به ظاهر دشوار ضرب ، مبنای معمول ترین روش رمزنگاری امروزی یعنی ، دستگاه  RSA است . اعداد اول مورد استفاده در این سیستم 100 رقمی هستند .

یکی از عادی ترین راه های شناسایی اعداد اول ، تقسیم آن به اعداد دیگر است . اگر بر هیچ عددی غیر از خودش و یک بخشپذیر نبود ، پس اول است . از طرفی مشخص می شود که اعداد زوج اول نیستند چون بر دو بخشپذیرند ، همچنین اعدادی که جذر دقیق دارند نیز اول نیستند . اما مشخص است که این روش ها بیفایده هستند . به عنوان مثال اگر عدد اولی دارای صد رقم باشد در آن صورت کل عمر باقیمانده از کیهان ، طبق نظریه های جدید کیهان شناسی نیز برای مشخص کردن اول بودن این عدد با این روش ها کفایت نمی کند  ! 

بنابراین ریاضیدانان به سراغ روشهای دیگر رفته‌اند.  مهمترین سوال در مورد همه این روشها آن است كه با چه سرعتی می‌توانند یك عدد اول را مشخص كنند و با ازدیاد ارقام عدد اول زمان لازم برای محاسبه چه اندازه طولانی تر می شود. اگر به عنوان مثال زمان محاسبه به توان ثابتی از شمار ارقام عدد ازدیاد یابد در آن صورت این روش روش قابل قبولی به شمار آورده می‌شود . به این نوع روشها كه زمان به صورت توانی در آنها افزوده می‌شود روشهای توانی می‌گویند. روشهای دیگر كه زمان در آنها با سرعت بیشتری افزایش می‌یابد روشهای غیرتوانی نام دارند.  

بزرگترین عدد کشف شده برابر با دو به توان  43112609 منهای یک است . این عدد یک عدد مرسن است . عدد مرسن ، عددی اول به شکل زیر است :

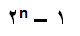
که n یک عدد طبیعی است .

 حامی مالی جستجوگران اعداد اول با بیش از ده میلیون رقم بنیاد

  (Electronic Frontier Foundation)

که به اختصار ( EFF ) خوانده می شود ، است . جوایزی که این بنیاد برای یابندگان در نظر گرفته است ، بالای صد هزار دلار است .

اگر می خواهید عددی را برای آول بودن تست کنید ، روی لینک زیر کلیک کنید .

تست اعداد اول